How Newton Derived the Shape of Earth
To argue for universal gravitation, Newton had to become a “geodesist.”

Isaac Newton’s landmark 1687 work, “Philosophiæ Naturalis Principia Mathematica,” laid the groundwork for classical mechanics, describing the laws of gravitation and predicting astronomical phenomena, like the movement of planets. The work changed physics.
But buried in the Principia is an often-overlooked triumph: Newton’s derivation of Earth’s figure — that is, the calculation of its shape, size, and surface gravity variation, part of a field later known as geodesy — which was crucial to his argument for universal gravitation. Here, I reconstruct Newton’s derivation and its significance1.
Newton’s derivation
Newton began his quantitative derivation of Earth’s figure in 1686, after learning about work by the French physicist Jean Richer. In 1671, Richer had traveled to Cayenne, the capital of French Guiana in South America, and experimented with a pendulum clock. Richer found that the clock, calibrated to Parisian astronomical time (48°40’ latitude), lost an average of 2.5 minutes per day in Cayenne (5° latitude). This was surprising, but it could be explained by the theory of centrifugal motion, recently developed by Christian Huygens: The theory suggested that the centrifugal effect is strongest at the equator, so the net effective surface gravity would decrease as you moved from Paris to Cayenne2.
Newton accepted Huygens’s theory but realized it meant something strange: If Earth is a sphere and its centrifugal effect is strongest at the equator, gravity would vary across Earth’s surface, and the ocean would bulge up at the equator — a proposition that Newton considered absurd.
To resolve this, he proposed that the solid Earth had behaved like a fluid throughout its formation, gradually bulging up at the equator because of the centrifugal effect. He proposed modeling planets as rotating fluids in equilibrium, where the planet’s shape is stable while the force generated by its rotational motion, and the gravitational attraction between its particles, acts on it3.
To derive Earth’s figure based on this theory, Newton first had to calculate the ratio between gravitational acceleration and centrifugal force at the equator (a 1-to-290.8 ratio), based on the period of Earth’s diurnal rotation and estimates of Earth’s equatorial diameter. Newton knew the length of two meridional arcs that he could use for this calculation, measured by surveyors in England and France. He calculated gravitational acceleration at the equator from Richer’s pendulum measurements at 48°50’ latitude, extrapolating the corresponding value at the equator of a homogeneous sphere4.
Equipped with the ratio, Newton faced a problem: How could he express mathematically that a rotating fluid, whose constituents attract according to a certain law of gravity, is in a state of equilibrium? To answer this, Newton used an ingenious thought experiment, which he had developed in his 1685 “Liber Secundus” manuscript5: A rotating body is in a state of hydrostatic equilibrium if the weight of water in two channels x and y, where x connects the equator to Earth’s center and y connects Earth’s center to one of the poles, is identical. Since x is affected by the centrifugal effect, equilibrium is fulfilled if the overall centrifugal “pull” on the equator is compensated by a change to the figure. In other words, the equatorial regions need to “bulge up” and the poles “flatten” to such an extent that the total weight of x and y (i.e., net gravitational attraction toward the center) is the same. This attempt to define hydrostatic equilibrium was later named the “principle of canals6” (Fig. 1).
Newton then used his theory of gravitational attraction to derive the figure that a rotating body would need to have to balance the net attraction on the two columns — more precisely, the ratio between equatorial diameter and polar axis that would fulfill equilibrium. To calculate this, Newton determined the ratio7 between polar and equatorial surface gravity for the simpler case of a non-rotating oblate figure, with the axis-diameter ratio of 100-to-101, arriving at 501-to-500.
If this result is multiplied by the length of the two fluid columns (100-to-101), we obtain the ratio of 501-to-505 between the net gravitational forces acting on the polar and equatorial fluid columns. Therefore, the net gravitational force acting on the equatorial fluid column is greater than the corresponding net force acting on the polar fluid column by a magnitude of 4-to-505. So, if a spheroid with the dimensions of 100-to-101 is rotating and in a state of hydrostatic equilibrium, the ratio between equatorial surface gravity and centrifugal force must be 4-to-505.
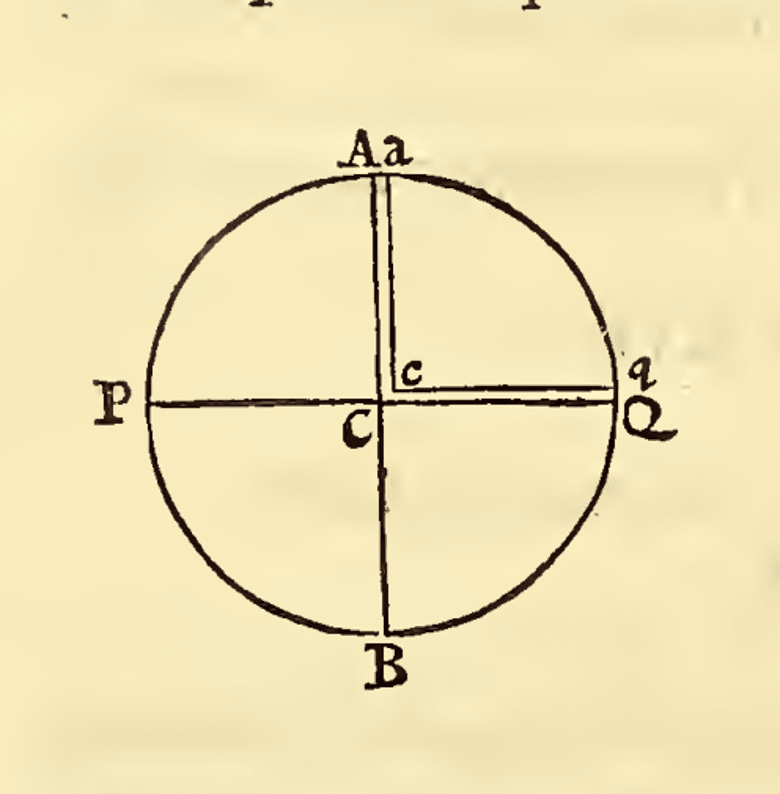
Since Newton’s premise was that Earth is in a state of hydrostatic equilibrium, he extended this thought experiment to Earth. For his previously determined 1-to-290.1 ratio between equatorial surface gravity and centrifugal force, he calculated a corresponding polar axis and equatorial diameter ratio of 689-to-692. He concluded that Earth, modeled as a homogeneous spheroid that rotates with uniform angular velocity, must have polar and equatorial axes with a length ratio of 689-to-692 to be in a state of hydrostatic equilibrium.
He then calculated the effective surface gravity for this model of Earth — indicated by the length of the seconds-pendulum — to vary as the square of the sine of the latitude8. By deriving a general latitudinal variation, he was no longer just concerned with the length ratio between the equatorial diameter and polar axis; instead, he was modeling Earth’s overall figure — an oblate ellipsoid with an ellipticity of 3-to-692 (about 1-to-230.7). Using the pendulum length at 48°40’ astronomical latitude in Paris as a reference point, he predicted that the pendulum has to be shortened by 81/1000 and 89/1000 inches in Gorée and Cayenne, respectively, to preserve its period — close but still inaccurate approximations of the measurements (100/1000 and 125/1000 inches).
Earth’s figure and universal gravitation
Clearly, Newton invested considerable effort in deriving Earth’s figure and latitudinal variation in surface gravity. Besides presenting a novel definition for the hydrostatic equilibrium of rotating bodies, these results presumed Newton’s theory of gravitational attraction. His predictions only hold if all of Earth’s constituent particles mutually attract. Hence, his predictions offered a test for the most fundamental and novel assumption in Newton’s theory of gravitation: that gravity acts universally between all particles of matter. In fact, as George Smith showed, these predictions are the Principia’s only such test9.
Newton was aware of this. His editor Roger Cotes kept pushing him to revise the geodetic results in light of new data10, and in the second edition of the Principia, Newton revised Earth’s ellipticity from a 689-692 ratio to a 1-to-230 ratio and added a table with detailed predictions of measurements for surface gravity and surface curvature11. Newton revised these predictions again for the third edition (Fig. 2).
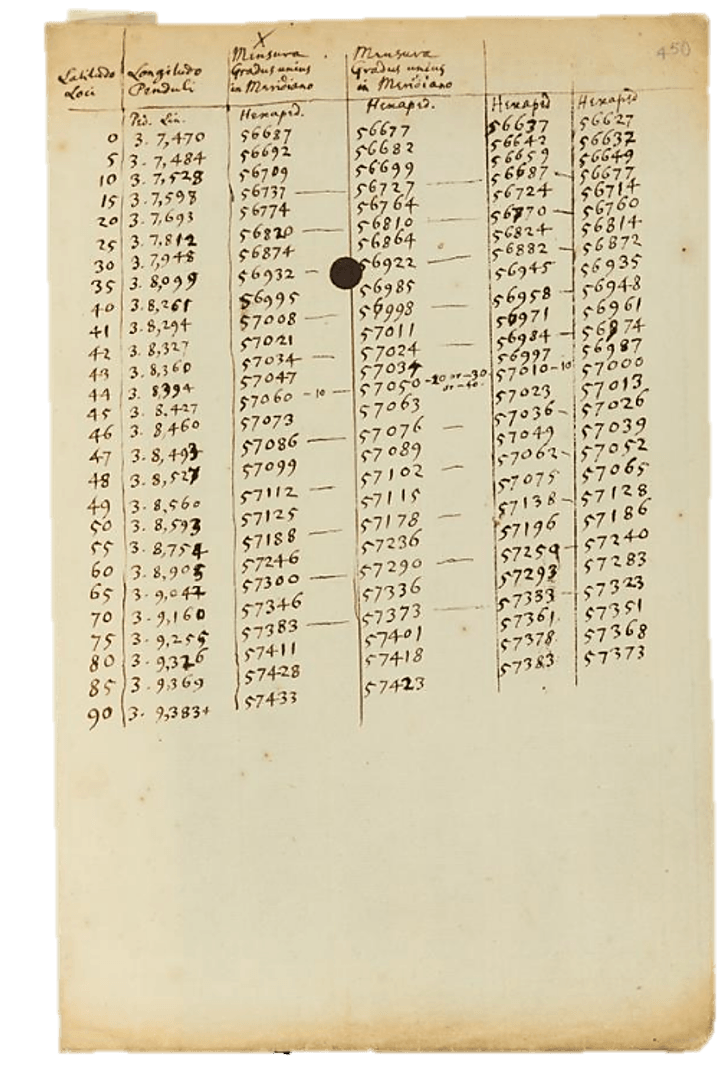
Were Newton’s geodetic predictions accurate enough to reflect their importance in his argument for universal gravitation? On a naïve reading, the answer is no. When the third and last edition of the Principia was published, Newton had access to one arc measurement of the latitudinal variation in the length of 1° of meridian and five pendulum measurements of the variation of surface gravity with latitude. The arc measurement disagreed with Newton’s predictions, seeming to indicate that Earth is an oblong, rather than oblate, spheroid. Out of existing pendulum measurements, only Jean Richer’s seemed similar, but even that still disagreed with Newton’s prediction. The prediction also does not match current data: Satellite measurements indicate that Earth’s ellipticity has a ratio of 1-to-298.25722356312.
However, such a pessimistic view of Newton’s geodetic work misses important nuances of the Principia. As George Smith has argued, the Principia not only proposes theoretical predictions, but a methodology of testing through approximation. Newton accepted that his predictions would likely be inaccurate because he relied on uncertain background hypotheses when deriving them. The success of the universal theory of gravitation, then, should not be measured by the immediate agreement between initial predictions and measurements. Rather, Newton intended that his theory be tested on how well it could guide adjustments to background hypotheses, leading to converging measurements13.
In other words, Newton did not aim to establish Earth’s figure once and for all. Rather, he gave approximations, which would allow for adjustments to the assumptions he made in his derivation. With Newton’s early derivation, for example, he assumed the rotating Earth has a homogeneous density. But when his predictions and Richer’s measurements in Cayenne and Gorée disagreed, he modified this assumption in the first edition of the Principia. If Earth is denser at its center, he suggested, the ellipticity of Earth’s equilibrium figure and its surface gravity variation will differ.
With this methodology, Newton passed the torch to future researchers, inviting them to develop hypotheses that would work with these initial measurements, and could then be tested with increasingly precise measurements14.
In line with Newton’s methodology, geodesists eventually produced convergent measurements of Earth’s ellipticity based on variation in latitudinal surface gravity and curvature. For about two and a half centuries, they used the theories of gravitation and hydrostatic equilibrium to model Earth’s figure, motion, and constitution, and gradually revised these parameters in light of new measurements. By 1909, all major ellipticity measurements converged within 297.6±0.9, implying that density increased inward15. By 1926, Viennese astronomer Samuel Oppenheim concluded that these results offered overwhelming evidence for Newtonian gravity on Earth, vindicating both Newton’s theory of gravitation and his methodology16.
For Ohnesorge’s full essay and his reconstruction of Newton’s derivation, visit go.aps.org/geodesy. Learn more about Ohnesorge’s research at mohnesorgehps.com.
Other Sources
Subrahmanyan Chandrasekhar, Newton’s Principia for the Common Reader (Clarendon Press, 2003).
Alexis Claude Clairaut, "I. An Inquiry Concerning the Figure of Such Planets as Revolve about an Axis," Philosophical Transactions of the Royal Society of London 40, 449 (1738): 277–306.
John Greenberg, ‘Isaac Newton and the Problem of the Earth’s Shape’. Archive for History of Exact Sciences 49, vol. 4 (1996): 371–91.
Mary Terrall, The Man Who Flattened the Earth: Maupertuis and the Sciences in the Enlightenment (Univ. of Chicago Press, 2002).
The Mathematical Works of Isaac Newton, ed. Derek Thomas Whiteside, vol. 6 (Cambridge University Press, 1974).
"Closing the Loop: Testing Newtonian Gravity, Then and Now," in Newton and Empiricism, ed. Zvi Biener and Eric Schliesser, vol. 262–353 (Oxford Univ. Press, 2014).
Miguel Ohnesorge
Miguel Ohnesorge is a doctoral student at the University of Cambridge and visiting Fellow at Boston University’s Philosophy of Geoscience Lab.
The only published discussions of the work’s methodological importance are in Schliesser and Smith 2000 and Smith 2014, who do not reconstruct Newton’s derivation. Todhunter 1873 and Greenberg 1996 discuss the derivation in plain English, without methodological contextualization. Chandrasekhar 2003 also reconstructs the derivation in modern algebra, which contains some minor but confusing mistakes and ambiguities.
Christian Huygens, "Discours de La Cause de La Pesanteur," in Traité de Lumierè Avec Discours de La Cause de La Pesanteur, ed. Christian Huygens (Leiden: Pierre Vander, 1690).
The Principia: Mathematical Principles of Natural Philosophy, trans. Bernhard Cohen and Ann Whitman (Univ. of California Press, 1999).
The Principia
Isaac Newton, De moto Corporum Liber Secundus (Cambridge Univ. Library, MS Add. 3990, 1685).
Isaac Todhunter, A History of the Mathematical Theories of Attraction and the Figure of the Earth, from the Time of Newton to That of Laplace, vol. 1 (London: Macmillan, 1873).
Newton’s derivation for the attraction of perfectly spherical and spheroidal compound bodies is given in Book 1, Prop. 91, coroll. 1 and 2 and reconstructed in its original notation at go.aps.org/geodesy.
The Principia
Eric Schliesser and George E. Smith, "Huygens’s 1688 Report to the Directors of the Dutch East India Company on the Measurement of Longitude at Sea and the Evidence It Offered Against Universal Gravity," preprint (2000).
Cotes to Newton, The Correspondence of Isaac Newton, vol. 5 (1712): 232-236.
The Principia
World Geodetic System (WGS) 84 Model.
George E. Smith, "Essay Review: Chandrasekhar’s Principia: Newton’s Principia for the Common Reader," Journal for the History of Astronomy 27, vol. 4 (1996): 353–62.
The Principia
Miguel Ohnesorge, "Pluralizing Measurement: Physical Geodesy’s Measurement Problem and Its Resolution, 1880-1924," Studies in History and Philosophy of Science Part A (forthcoming).
A. Sommerfeld and Samuel Oppenheim, Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen: Fünfter Band: Physik (Vieweg+Teubner Verlag, 1926).